目次
正規分布とは
正規分布(ガウス分布)は、統計学において重要な確率分布の一つです。データの分布が、平均値を中心に左右対称に広がる形をした「ベルカーブ」になります。多くの自然現象や社会現象は、この正規分布に従うことが多いため、様々な分野で広く使われています。平均値を $\mu$、分散を $\sigma^2$ として $N(\mu, \sigma^2)$ と表し、特に $\mu=0$、$\sigma^2=1$ とした $N(0, 1)$ は標準正規分布といいます。分散 $\sigma^2$ に平方根 $\sqrt{}$ をかけた $\sigma$ は標準偏差と呼ばれます。分散も標準偏差もデータのばらつきを意味しますが、標準偏差はデータと同じ単位の指標になります。
正規分布の例
- 身長と体重
多くの集団における人の身長や体重は、正規分布に近い形をしています。例えば、成人男性の平均身長が170cmだとすると、160cmや180cm付近の人が多く、極端に低い人や高い人は少なくなります。 - 試験の点数
ある大規模な試験の成績も、しばしば正規分布に従います。平均点付近に多くの学生が集中し、非常に高得点や非常に低得点の学生は少ないです。
確率密度関数
正規分布の確率密度関数は、以下のように表されます:
$\begin{align*}
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right), \quad -\infty < x < \infty
\end{align*}$
68-95-99.7の法則
正規分布には68-95-99.7の法則と呼ばれる、データの散らばり方を示す経験則があります。これは、平均値を中心にデータがどの範囲に収まるかを示すもので、以下の確率が成り立ちます。
±1σの範囲に約68%のデータが含まれる
±2σの範囲に約95%のデータが含まれる
±3σの範囲に約99.7%のデータが含まれるこれは標準正規分布に限らず、一般の正規分布にも適用できます。
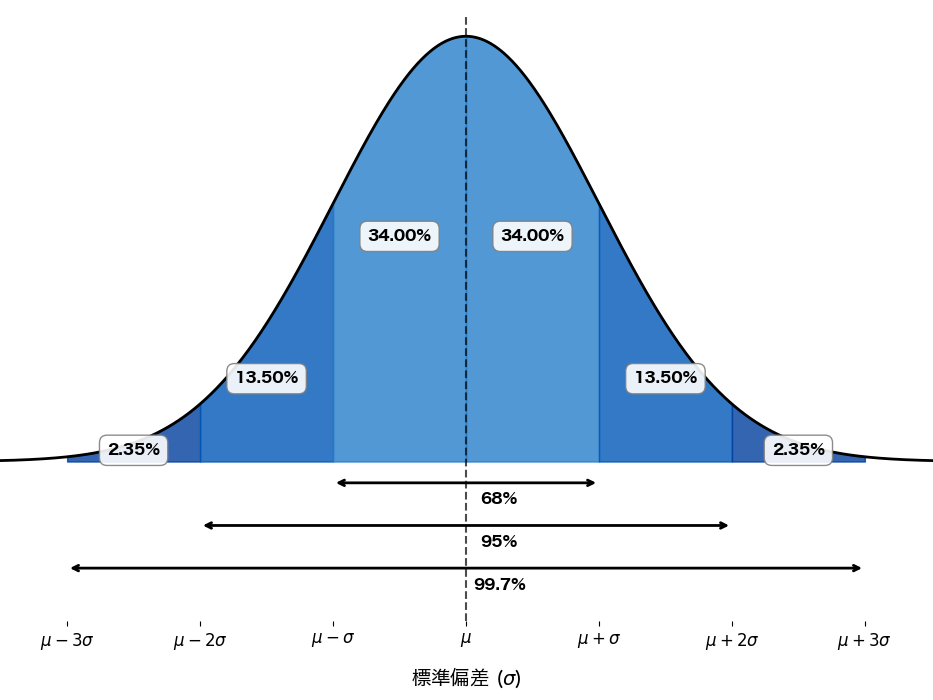
例えばある集団の身長が $N(170, 10^2)$ に従うとすると、次のことが言えます。
- 160cm~180cm $(\pm1\sigma)$ に約68%の人がいる
- 150cm~190cm $(\pm2\sigma)$ に約95%の人がいる
- 140cm~200cm $(\pm3\sigma)$ に約99.7%の人がいる
この法則は、異常値の検出や品質管理(6シグマ手法)にも応用されます。
期待値とその導出
正規分布の期待値は、以下のように表されます:
$E[X] = \mu$
実際に導出してみましょう。
$\begin{align*}
E[X] &= \int_{-\infty}^{\infty}xf(x)dx\\
&= \int_{-\infty}^{\infty}x\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx
\end{align*}$
ここで、$\begin{align*}\frac{x-\mu}{\sigma}=t\end{align*}$ と置くと、$dx = \sigma dt$
$\begin{align*}
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}(\sigma t + \mu)\exp\left(-\frac{t^2}{2}\right)\sigma dt\\
&= \frac{\sigma}{\sqrt{2\pi\sigma^2}}\left(\int_{-\infty}^{\infty}\sigma t\exp\left(-\frac{t^2}{2}\right)dt +
\int_{-\infty}^{\infty}\mu\exp\left(-\frac{t^2}{2}\right)dt\right)\\
&= \frac{\sigma}{\sqrt{2\pi\sigma^2}}\left(\sigma\int_{-\infty}^{\infty} t\exp\left(-\frac{t^2}{2}\right)dt +
\mu\int_{-\infty}^{\infty}\exp\left(-\frac{t^2}{2}\right)dt\right)\\
&= \frac{\sigma}{\sqrt{2\pi\sigma^2}}\left(\sigma[-e^{-\frac{t^2}{2}}]_{-\infty}^{\infty} + \mu\sqrt{2\pi}\right)
\end{align*}$
ここで、二つ目の積分はガウス積分を利用して変形しています。
$\begin{align*}
&= \frac{\sigma}{\sqrt{2\pi\sigma^2}}\mu\sqrt{2\pi}\\
&= \mu
\end{align*}$
分散とその導出
正規分布の分散は、以下のように表されます:
$V[X] = \sigma^2$
実際に導出してみましょう。
まずは、$E[X^2]$ を求めます。
$\begin{align*}
E[X^2] &= \int_{-\infty}^{\infty}x^2f(x)dx\\
&= \int_{-\infty}^{\infty}x^2\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx
\end{align*}$
ここで、$\begin{align*}\frac{x-\mu}{\sigma}=t\end{align*}$ と置くと、$dx = \sigma dt$
$\begin{align*}
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}(\sigma t + \mu)^2\exp\left(-\frac{t^2}{2}\right)\sigma dt\\
&= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}(\sigma^2 t^2 + 2\sigma t\mu + \mu^2)\exp\left(-\frac{t^2}{2}\right)dt\\
&= \frac{1}{\sqrt{2\pi}}\left(\int_{-\infty}^{\infty}\sigma^2 t^2\exp\left(-\frac{t^2}{2}\right)dt +
\int_{-\infty}^{\infty}2\sigma t\mu\exp\left(-\frac{t^2}{2}\right)dt+
\int_{-\infty}^{\infty}\mu^2\exp\left(-\frac{t^2}{2}\right)dt\right)\\
&= \frac{1}{\sqrt{2\pi}}\left(\int_{-\infty}^{\infty}\sigma^2 t^2\exp\left(-\frac{t^2}{2}\right)dt +
\int_{-\infty}^{\infty}\mu^2\exp\left(-\frac{t^2}{2}\right)dt\right)\\
&= \frac{1}{\sqrt{2\pi}}\left(\sigma^2\int_{-\infty}^{\infty} tt\exp\left(-\frac{t^2}{2}\right)dt +\mu^2\sqrt{2\pi}\right)
\end{align*}$
ここで、$\begin{align*}\int_{-\infty}^{\infty} tt\exp\left(-\frac{t^2}{2}\right)dt\end{align*}$を、部分積分を使って計算します。
$\begin{align*}
\int_{-\infty}^{\infty} tt\exp\left(-\frac{t^2}{2}\right)dt &= \left[-t\exp\left(-\frac{t^2}{2}\right)\right]_{-\infty}^{\infty}-\int_{-\infty}^{\infty} -\exp\left(-\frac{t^2}{2}\right)dt \\
&= \sqrt{2\pi}
\end{align*}$
この結果を元の式に入れて、
$\begin{align*}
\frac{1}{\sqrt{2\pi}}\left(\sigma^2\int_{-\infty}^{\infty} tt\exp\left(-\frac{t^2}{2}\right)dt +\mu^2\sqrt{2\pi}\right) &= \frac{1}{\sqrt{2\pi}}\left(\sigma^2\sqrt{2\pi} +\mu^2\sqrt{2\pi}\right)\\
&= \sigma^2 + \mu^2
\end{align*}$
よって、
$\begin{align*}
V[X] &= E[X^2]-E[X]^2\\
&= \sigma^2 + \mu^2-(\mu)^2\\
&= \sigma^2
\end{align*}$
モーメント母関数とその導出
正規分布のモーメント母関数は、以下のように表されます:
$\begin{align*}M(t) = E[e^{tX}] = \exp\left(\mu t + \frac{\sigma^2t^2}{2}\right), \quad -\infty < t < \infty\end{align*}$
実際に導出してみましょう。
$\begin{align*}
M(t) &= \int_{-\infty}^{\infty}e^{tx}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx\\
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2} + tx\right)dx\\
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{x^2-2x(\mu + \sigma^2t) + \mu^2}{2\sigma^2}\right)dx
\end{align*}$
平方完成を行います。
$\begin{align*}
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{(x-(\mu+\sigma^2 t))^2 + \mu^2-(\mu + \sigma^2 t)^2}{2\sigma^2}\right)dx\\
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{(x-(\mu+\sigma^2 t))^2-2\mu\sigma^2 t-\sigma^4 t^2}{2\sigma^2}\right)dx\\
&= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2}\right)\exp\left(\mu t + \frac{\sigma^2 t^2}{2}\right)dx\\
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2}\right)\frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp\left(-\frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2}\right)dx\\
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2}\right)\frac{1}{\sqrt{2\pi\sigma^2}}\sqrt{2\sigma^2\pi}\\
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2}\right)
\end{align*}$
正規分布の再生性
正規分布には再生性という性質があります。これは、二つの独立な確率変数 $X_1 \sim N(\mu_1, \sigma_1^2)$ と $X_2 \sim N(\mu_2, \sigma_2^2)$ の和 $X_1 + X_2$ も正規分布 $N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$ に従う性質です。
これは $X_1 + X_2$ のモーメント母関数が、
$\begin{align*}
E[e^{t(X_1+X_2)}] &= E[e^{tX_1}e^{tX_2}] = E[e^{tX_1}]E[e^{tX_2}]\\
&= \exp{\left(\mu_1 t + \frac{\sigma_1^2 t^2}{2}\right)}\exp{\left(\mu_2 t + \frac{\sigma_2^2 t^2}{2}\right)}\\
&= \exp{\left((\mu_1+\mu_2)t+\frac{(\sigma_1^2+\sigma_2^2)t^2}{2}\right)}
\end{align*}$
となることから分かります。
再生性については確率分布の再生性でも解説しているので、併せてご覧ください。
標準正規分布とカイ二乗分布の関係性
標準正規分布はカイ二乗分布($\chi^2$ 分布)と密接な関係があります。カイ二乗分布は、標本分散の分布に関係し、統計的推測のさまざまな場面で利用されます。
カイ二乗分布は、互いに独立な標準正規分布に従う $k$ 個の確率変数の二乗和として定義されます。
定義:$Z_1, Z_2, \dots , Z_k$ が互いに独立に標準正規分布 $N(0, 1)$ に従うとすると、
$\begin{align*}X = Z_1^2 + Z_2^2 + \dots + Z_k^2\end{align*}$
は自由度 $k$ のカイ二乗分布 $\chi^2(k)$ に従います。
まとめ
正規分布は、データ分析や統計学で非常に重要な分布です。データの中心傾向やばらつきを理解する上で、正規分布は役立ちます。身近な例や実世界の現象でよく見られるため、データが正規分布に従っているかどうかを確認することは、統計的な分析の第一歩となります。

