負の二項分布とは
負の二項分布は、繰り返し行われる成功確率 $p$ のベルヌーイ試行において、$r$ 回目の成功が起こった時点までに起きた失敗の回数を扱うもので、$NB(r, p)$ と表します。二項分布と名前は似ていますが、二項分布は固定された回数のベルヌーイ試行の中で成功の回数を数える分布ですが、負の二項分布は決められた成功回数に達するまでにかかる失敗の数に注目するという点で異なります。この分布の特徴から、$NB(r, p)$ の成功回数を1にした $NB(1, p)$ は幾何分布になります。
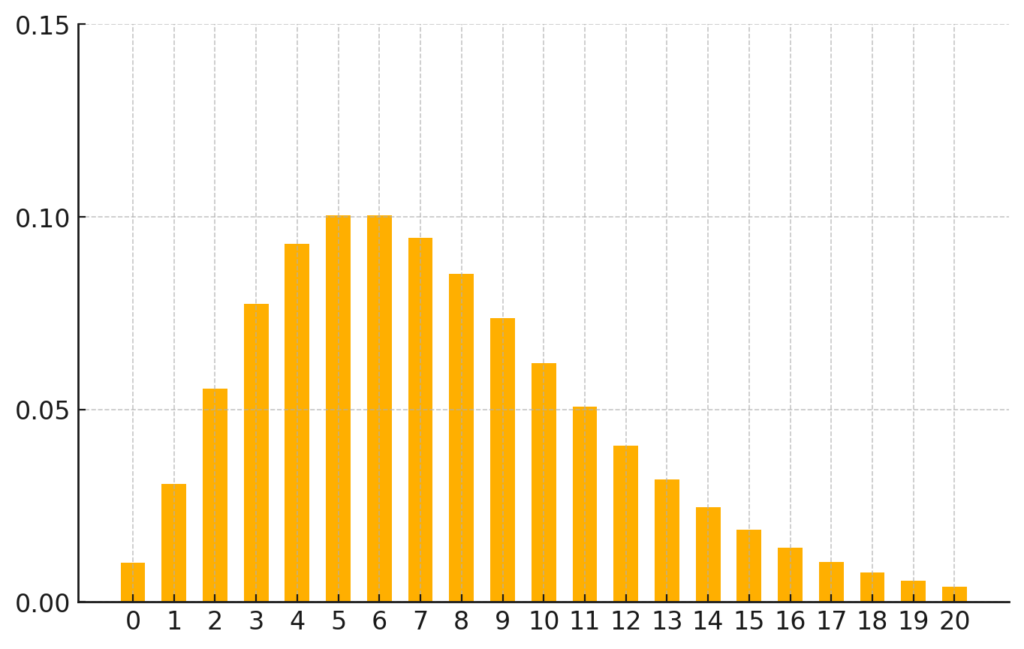
負の二項分布の例
- 顧客獲得マーケティング
あるマーケティングキャンペーンにおいて、何回のアプローチを行えば特定の数の新規顧客を獲得できるか、という問題に適用されます。例えば、特定の製品を売り込む際に、10人の顧客が購入するまでに何回失敗(断られるか)が起こるかを予測するのに利用できます。 - 臨床試験
臨床試験において、薬の効果が確認されるまでに何回の無効な試験(失敗)が必要か、といった場合にも使用されます。これは、ある回数の成功を得るまでに発生する試行の数をモデル化する際に有効です。
確率関数
負の二項分布の確率関数は、以下のように表されます:
$\begin{align*}P(X=x) = \binom{x+r-1}{x}p^r (1-p)^x\end{align*}$
ここで、
- $P(X=x)$ は、確率変数 $X$ が特定の値 $x$ をとる確率を表します。
- $\begin{align*}\binom{x+r-1}{x}\end{align*}$ は $x+r-1$ 回の試行のうち $x$ 回失敗する場合の組み合わせの数を表す二項係数であり、
$\begin{align*} \binom{x+r-1}{x} = {}_{x+r-1}C_{x} \\
= \frac{(x+r-1)!}{x!((x+r-1)-x)!} \end{align*}$
です。
期待値とその導出
負の二項分布の期待値は、以下のように表されます:
$\begin{align*}E[X] = \frac{r(1-p)}{p}\end{align*}$
実際に導出してみましょう。
$\begin{align*}
E[X] &= \sum_{x=0}^{\infty}xP(X=x)\\
&= \sum_{x=0}^{\infty}x\binom{x+r-1}{x}p^r (1-p)^x\\
&= \sum_{x=0}^{\infty}\frac{(x+r-1)!}{x!((x+r-1)-x)!}xp^r (1-p)^x\\
&= \sum_{x=1}^{\infty}\frac{(x+r-1)!}{(x-1)!(r-1)!}p^r (1-p)^x\\
&= \sum_{x=1}^{\infty}\frac{(x+r-1)!}{(x-1)!r!}r\frac{p^{r+1}}{p}(1-p)^{x-1}(1-p)\\
&= \frac{r(1-p)}{p}\sum_{x=1}^{\infty}\frac{(x+r-1)!}{(x-1)!r!}p^{r+1}(1-p)^{x-1}\\
&= \frac{r(1-p)}{p}\sum_{x=1}^{\infty}\binom{x+r-1}{x-1}p^{r+1}(1-p)^{x-1}
\end{align*}$
ここで、右辺の $\Sigma$ 以降は負の二項分布の確率関数になっています。したがって確率の第二の公理より、
$\begin{align*}
&= \frac{r(1-p)}{p}
\end{align*}$
分散とその導出
負の二項分布の分散は、以下のように表されます:
$\begin{align}V[X] = \frac{r(1-p)}{p^2}\end{align}$
実際に導出してみましょう。
まずは、$E[X^2]$ を求めます。
$\begin{align*}
E[X^2] &= \sum_{x=0}^{\infty}x^2P(X=x)\\
&= \sum_{x=0}^{\infty}x^2\binom{x+r-1}{x}p^r (1-p)^x\\
&= \sum_{x=1}^{\infty}x\frac{(x+r-1)!}{(x-1)!(r-1)!}p^r(1-p)^x\\
&= \frac{r(1-p)}{p}\sum_{x=1}^{\infty}x\frac{(x+r-1)!}{(x-1)!r!}p^{r+1}(1-p)^{x-1}\\
&= \frac{r(1-p)}{p}\sum_{x=1}^{\infty}((x-1)+1)\frac{(x+r-1)!}{(x-1)!r!}p^{r+1}(1-p)^{x-1}\\
&= \frac{r(1-p)}{p}\left(\sum_{x=1}^{\infty}(x-1)\frac{(x+r-1)!}{(x-1)!r!}p^{r+1}(1-p)^{x-1} + \sum_{x=1}^{\infty}\frac{(x+r-1)!}{(x-1)!r!}p^{r+1}(1-p)^{x-1}\right)\\
&= \frac{r(1-p)}{p}\left(\frac{(r+1)(1-p)}{p} + 1\right)
\end{align*}$
最後の式変形は、負の二項分布の期待値と確率の第二の公理を利用しています。
よって、
$\begin{align*}
V[X] &= E[X^2]-E[X]^2\\
&= \frac{r(1-p)}{p}\left(\frac{(r+1)(1-p)}{p} + 1\right)-\left(\frac{r(1-p)}{p}\right)^2\\
&= \frac{(r^2+r)(1-p)^2}{p^2}+\frac{rp(1-p)}{p^2}-\frac{r^2(1-p)^2}{p^2}\\
&= \frac{r(1-p)}{p^2}
\end{align*}$
確率母関数とその導出
負の二項分布の確率母関数は、以下のように表されます:
$\begin{align}G(s) = E[s^X] = \left(\frac{p}{1-(1-p)s}\right)^r\end{align}$
実際に導出してみましょう。
$\begin{align*}
G(s) &= \sum_{x=0}^{\infty}s^x\binom{x+r-1}{x}p^r(1-p)^x\\
&= p^r\sum_{x=0}^{\infty}\binom{x+r-1}{x}(s(1-p))^x\\
&= p^r\frac{1}{(1-s(1-p))^r}\\
&= \left(\frac{p}{1-(1-p)s}\right)^r
\end{align*}$
最後は、二項級数の公式を適用しています。
この確率母関数から、負の二項分布は再生性を持つことが分かります。つまり $X_1 \sim NB(r_1, p)$、$X_2 \sim NB(r_2, p)$ に関して、$X_1 + X_2 \sim NB(r_1 + r_2, p)$ となります。
再生性については確率分布の再生性でも解説しているので、併せてご覧ください。
まとめ
負の二項分布は、実世界の様々な場面で失敗と成功の関係をモデル化する際に役立つ強力なツールです。マーケティングから医療分野まで、負の二項分布は試行回数の変動に対応するための効果的な手法となっています。この分布の特徴を理解し、適切な場面で活用することで、より正確な予測や意思決定が可能になるでしょう。

