目次
幾何分布とは
幾何分布は、ある事象が初めて成功するまでの試行回数あるいは失敗回数を表し、$Geo(p)$ と書きます。例えば、コインを投げて初めて表が出るまでに何回投げたか、というような問題に関連しています。この分布は特に、成功確率が一定の独立したベルヌーイ試行の連続において適用されます。
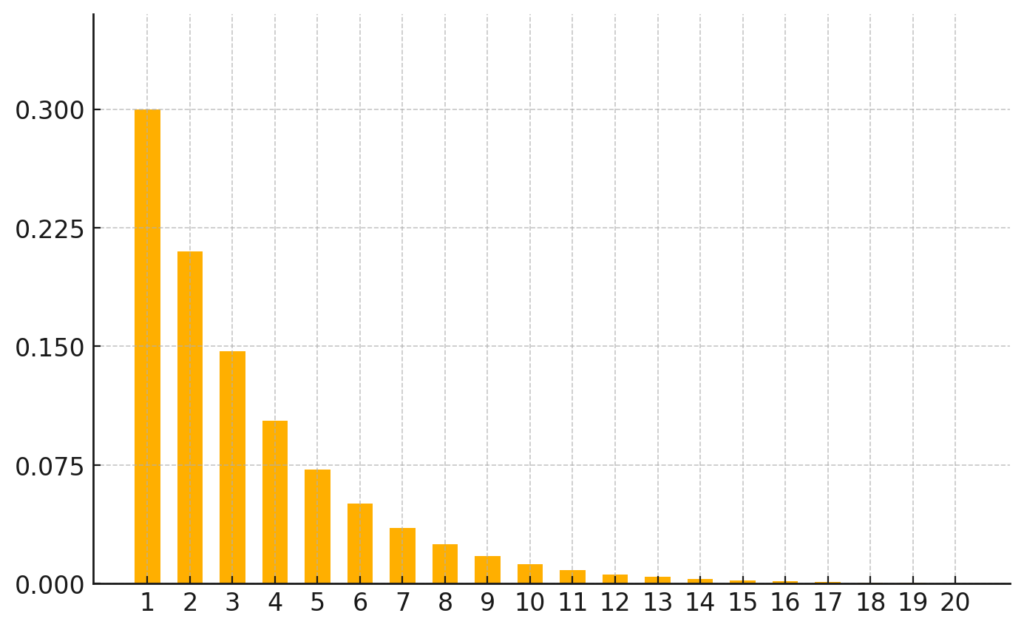
幾何分布の例
- 製品のテスト
ある製品の不良率が1%だと仮定します。最初に不良品が見つかるまでの製品の検査回数は、幾何分布に従うと考えられます。 - インタビュー調査
街頭インタビューで特定の条件を満たす人に出会うまでの回数も幾何分布を使ってモデル化できます。
確率関数
幾何分布の確率関数は、定義によって2通りの書き方があります。
定義1:初めて成功するまでに起こる失敗回数に着目する場合
$P(X=x) = p(1-p)^x, \quad x = 0, 1, 2, …$
定義2:初めて成功するまでに起こる試行回数に着目する場合
$P(X=x) = p(1-p)^{x-1}, \quad x = 1, 2, 3, …$
ここで、$P(X=x)$ は確率変数 $X$ が特定の値 $x$ をとる確率を表します。
期待値とその導出
幾何分布の期待値は定義によって変わります。定義ごとに見てみましょう。
定義1:初めて成功するまでに起こる失敗回数に着目する場合
$\begin{align*}E[X] = \frac{1-p}{p}\end{align*}$
実際に導出してみましょう。
$\begin{align*}
E[X] &= \sum_{x=0}^{\infty}xP(X=x)\\
&= \sum_{x=0}^{\infty}xp(1-p)^x\\
&= p\sum_{x=0}^{\infty}x(1-p)^x\\
&= p(1-p)\sum_{x=0}^{\infty}x(1-p)^{x-1}
\end{align*}$
ここで、$\begin{align*}\frac{1}{1-x}\end{align*}$ のマクローリン展開を考えます。
$\begin{align*}
\frac{1}{1-x} &= 1 + \frac{\left.\frac{1}{(1-x)^2}\right|_{x=0}}{1!}(x-0)^1 + \frac{\left.\frac{2}{(1-x)^3}\right|_{x=0}}{2!}(x-0)^2 + \frac{\left.\frac{6}{(1-x)^4}\right|_{x=0}}{3!}(x-0)^3 + … \\
&= 1 + x + x^2 + x^3 + …\\
&= \sum_{k=0}^{\infty}x^k
\end{align*}$
となります。さらにこの両辺を $x$ で微分すると、
$\begin{align*}
\frac{1}{(1-x)^2} = \sum_{k=0}^{\infty}kx^{k-1}
\end{align*}$
$x$ を $1-p$ 、$k$ を $x$ にすると、右辺はマクローリン展開前の$\Sigma$ 以降の式と一致します。これを利用すると、
$\begin{align*}
E[X] &= p(1-p)\frac{1}{(1-(1-p))^2}\\
&= p(1-p)\frac{1}{p^2}\\
&=\frac{1-p}{p}
\end{align*}$
定義2:初めて成功するまでに起こる試行回数に着目する場合
$\begin{align*}E[X] = \frac {1}{p}\end{align*}$
実際に導出してみましょう。導出過程は定義1と同様です。
$\begin{align*}
E[X] &= \sum_{x=0}^{\infty}xP(X=x)\\
&= \sum_{x=0}^{\infty}xp(1-p)^{x-1}\\
&= p\sum_{x=0}^{\infty}x(1-p)^{x-1}
\end{align*}$
ここで先ほどのマクローリン展開を利用して、
$\begin{align*}
&= p\frac{1}{(1-(1-p))^2}\\
&= p\frac{1}{p^2}\\
&= \frac{1}{p}
\end{align*}$
分散とその導出
幾何分布の分散は、定義1と2どちらも以下のように表されます:
$\begin{align*}V[X] = \frac{1-p}{p^2}\end{align*}$
実際に導出してみましょう。期待値や確率関数は定義1のものを使います。
まずは、$E[X^2]$ を求めます。
$\begin{align*}
E[X^2] &= \sum_{x=0}^{\infty}x^2P(X=x)\\
&= \sum_{x=0}^{\infty}x^2p(1-p)^x\\
&= p\sum_{x=0}^{\infty}x^2(1-p)^x
\end{align*}$
ここで、期待値の導出時に利用した $\begin{align*}\frac{1}{(1-x)^2} = \sum_{k=0}^{\infty}kx^{k-1}\end{align*}$ の両辺に $x$ を掛けて微分します。
$\begin{align*}
\left(\frac{x}{(1-x)^2}\right)’ &= \left(\sum_{k=0}^{\infty}kx^k\right)’\\
\frac{(1-x)^2-2x(1-x)(-1)}{(1-x)^4} &= \sum_{k=0}^{\infty}k^2x^{k-1}\\
\frac{1+x}{(1-x)^3} &= \sum_{k=0}^{\infty}k^2x^{k-1}
\end{align*}$
この両辺にさらに $x$ を掛けます。
$\begin{align*}
\frac{x(1+x)}{(1-x)^3} &= \sum_{k=0}^{\infty}k^2x^k
\end{align*}$
この式の $x$ を $1-p$ に、$k$ を $x$ に置き換えると、$E[X^2]$ が計算できます。
$\begin{align*}
E[X^2] &= p\sum_{x=0}^{\infty}x^2(1-p)^x\\
&= p\frac{(1-p)(1+(1-p))}{(1-(1-p))^3}\\
&= \frac{(1-p) + (1-p)^2}{p^2}
\end{align*}$
よって、
$\begin{align*}
V[X] &= E[X^2]-E[X]^2\\
&= \frac{(1-p) + (1-p)^2}{p^2}-\left(\frac{1-p}{p}\right)^2\\
&= \frac{1-p}{p^2}
\end{align*}$
確率母関数とその導出
幾何分布の確率母関数も定義によって変わります。定義ごとに見てみましょう。
定義1:初めて成功するまでに起こる失敗回数に着目する場合
$\begin{align*}G(s) = E[s^X] = \frac{p}{1-(1-p)s}\end{align*}$
実際に導出してみましょう。
$\begin{align*}
G(s) &= \sum_{x=0}^{\infty} s^xp(1-p)^x\\
&= p\sum_{x=0}^{\infty}((1-p)s)^x\\
&= p\frac{1}{1-(1-p)s}\\
&= \frac{p}{1-(1-p)s}
\end{align*}$
ここで、無限等比級数の公式を利用して変形しています。
定義2:初めて成功するまでに起こる試行回数に着目する場合
$\begin{align*}G(s) = \frac{ps}{1-(1-p)s}\end{align*}$
実際に導出してみましょう。
$\begin{align*}
G(s) &= \sum_{x=1}^{\infty} s^xp(1-p)^{x-1}\\
&= \sum_{x=1}^{\infty}s^xp\frac{(1-p)^x}{(1-p)}\\
&= \frac{p}{1-p}\sum_{x=1}^{\infty}s^x(1-p)^x\\
&= \frac{p}{1-p}\frac{(1-p)s}{1-(1-p)s}\\
&= \frac{ps}{1-(1-p)s}
\end{align*}$
幾何分布の無記憶性
幾何分布は無記憶性という性質を持っています。ある確率変数が無記憶性を持つとき、以下の式が成り立ちます。
$P(X \geq t + s | X \geq t) = P(X \geq s), \quad t, s = 0, 1, 2, …$
これは、ある試行で $t$ 回の失敗が起こった後でも、その後の試行でさらに $s$ 回失敗が続く確率が初めから $s$ 回失敗する確率と同じであるということを意味します。つまり、過去に何度失敗したかに関係なく次の試行の成功・失敗は独立しており、常に同じ確率で成功または失敗が続くという特性が幾何分布の無記憶性の本質です。
実際に無記憶性を示してみましょう。
「$X \geq t$」は「初めの $t$ 回が全て失敗」と同値であるため、$P(X \geq t) = (1-p)^t$ となります。したがって、
$\begin{align*}
P(X \geq t + s | X \geq t) = \frac{(1-p)^{t+s}}{(1-p)^t} = (1-p)^s = P(X \geq s)
\end{align*}$
まとめ
幾何分布は、成功するまでの試行回数や失敗回数をモデル化するために使われる確率分布です。製品の不良検出や調査における条件達成の回数など、さまざまな現実の問題に適用できます。この分布を理解することで、成功の確率やそのために必要な試行数に関する予測がより正確になります。

