離散一様分布とは
離散一様分布(Discrete Uniform Distribution)は確率分布の一種で、取りうる値が有限個あり、それぞれの値が等しい確率で発生する場合に用いられます。つまり、どの値が選ばれるかは等確率であり、結果に偏りがありません。
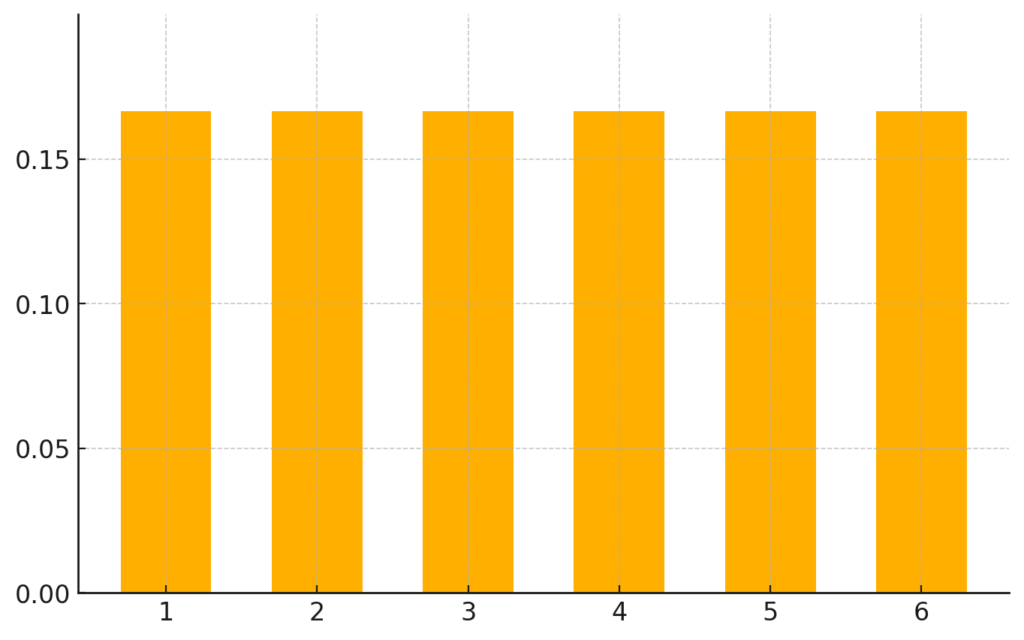
離散一様分布の例
- サイコロ
サイコロを振るとき、1から6の目が出る確率は全て等しく、$\begin{align*} \frac{1}{6} \end{align*}$です。つまり、どの目が出るかは完全にランダムで偏りがありません。 - トランプ
トランプのデッキから1枚のカードをランダムに引くと、スペード、ハート、ダイヤ、クラブの4つのスートが等しい確率、$\begin{align*} \frac{1}{4} \end{align*}$で選ばれます。
確率関数
離散一様分布の確率関数は、以下のように表されます:
$\begin{align*} P(X = x) = \frac{1}{N}, \quad x \in {x_1, x_2, \dots, x_N} \end{align*}$
ここで、
- $P(X = x)$ は、確率変数 $X$ が特定の値 $x$ をとる確率を表します。
- $N$ は取りうる値の数です。
期待値とその導出
離散一様分布の期待値は、以下のように表されます:
$\begin{align*} E[X] = \frac{N + 1}{2} \end{align*}$
実際に導出してみましょう。
$\begin{align*} E[X] &= \sum_{x=1}^{N} xP(X = x) \\ &= \sum_{x=1}^{N} x\frac{1}{N} \\ &= \frac{1}{N}\frac{1}{2}N(N + 1) \\ &=\frac{N + 1}{2} \end{align*}$
分散とその導出
離散一様分布の分散は、以下のように表されます:
$\begin{align*} V[X] = \frac{N^2-1}{12} \end{align*}$
実際に導出してみましょう。
まずは、$\begin{align*} E[X^2] \end{align*}$を求めます。
$\begin{align*} E[X^2] &= \sum_{x=1}^{N} x^2P(X = x) \\ &= \sum_{x=1}^{N} x^2\frac{1}{N} \\ &= \frac{1}{N}\frac{1}{6}N(N+ 1)(2N + 1) \\ &=\frac{(N + 1)(2N + 1)}{6} \end{align*}$
よって、
$\begin{align*} V[X] &= E[X^2]-E[X]^2 \\ &= \frac{(N + 1)(2N + 1)}{6}-\left(\frac{N + 1}{2} \right)^2 \\ &= \frac{N^2-1}{12} \end{align*}$
確率母関数とその導出
離散一様分布の確率母関数は、以下のように表されます:
$\begin{align*} G(s) = E[s^X] = \frac{s(1-s^N)}{N(1-s)} \end{align*}$
実際に導出してみましょう。
$\begin{align*}
G(s) &= \sum_{x=1}^{N} s^x \frac{1}{N} \\
&= \frac{1}{N}\sum_{x=1}^{N} s^x
\end{align*}$
ここで、等比級数の公式を使用します。
$\begin{align*}
&= \frac{1}{N} \frac{s(1-s^N)}{1-s} \\
&= \frac{s(1-s^N)}{N(1-s)}
\end{align*}$
まとめ
離散一様分布は、取りうる値が有限でどの値も等しい確率で発生する場合に使用されるシンプルな確率分布です。サイコロやカードゲームなど、日常的なランダムな事象を考える上でよく利用されます。公平性やランダム性をモデル化する上で重要なツールですが、現実にはわずかな偏りが生じる可能性がある点も理解しておく必要があります。

