連続一様分布とは
連続一様分布は、特定の範囲内の値が等しい確率で現れる分布を指します。これにより、その範囲内の任意の区間は、区間の幅に応じて同じ確率を持つことになります。例えば、ある区間 $[a, b]$ 内での連続一様分布 $U(a, b)$ は、その範囲内のどの値も均等に出現することが期待されます。
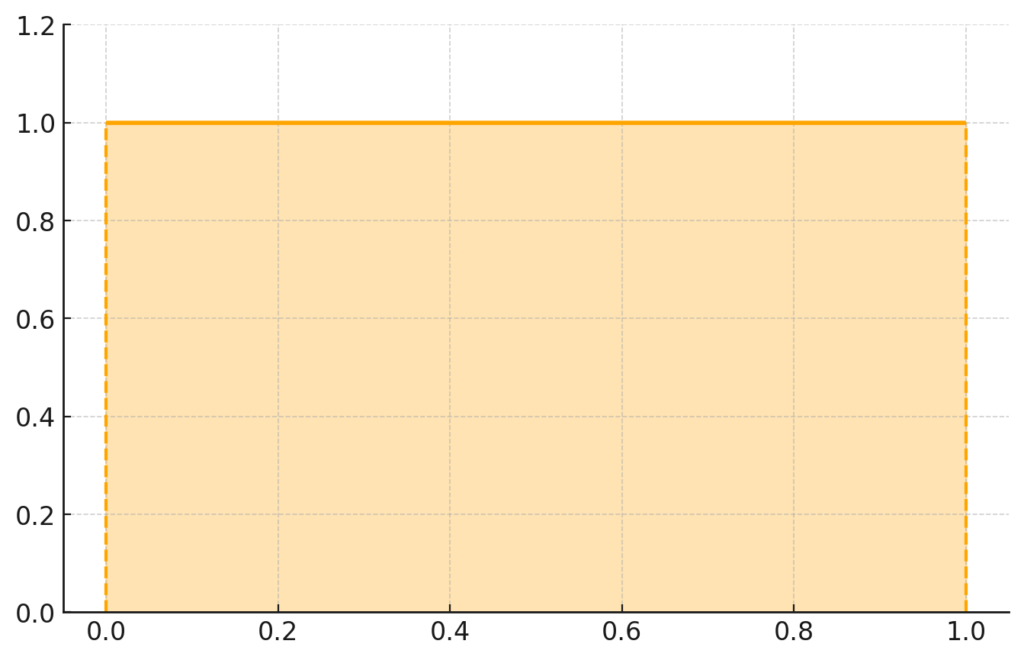
連続一様分布の例
- 乱数生成
コンピュータでランダムに数値を生成する際、多くの場合0から1の範囲内で連続一様分布に従う乱数を生成します。これは様々な確率分布に基づいたシミュレーションやモデリングの基本になります。 - 製造工程
製品の寸法がある範囲内でばらつく場合、連続一様分布がモデルとして使われることがあります。例えば、ある部品の長さが100mmから110mmの間で均等に分布する場合、その長さは連続一様分布に従うと考えられます。
確率密度関数
連続一様分布の確率密度関数は、以下のように表されます:
$f(x) =
\begin{cases}
\begin{align*}
&\frac{1}{b-a}&(a \leq x \leq b) \\
&\quad0&(\text{Others})
\end{align*}
\end{cases}$
期待値とその導出
連続一様分布の期待値は、以下のように表されます:
$\begin{align*}E[X] = \frac {a + b}{2}\end{align*}$
実際に導出してみましょう。
$\begin{align*}
E[X] &= \int_{a}^{b}xf(x)dx\\
&= \int_{a}^{b}x\frac{1}{b-a}dx\\
&= \frac{1}{b-a}\int_{a}^{b}xdx\\
&= \frac{1}{b-a}\left[\frac{x^2}{2}\right]_{a}^{b}\\
&= \frac{1}{b-a}\left(\frac{b^2-a^2}{2}\right)\\
&= \frac{1}{b-a}\frac{(b-a)(b+a)}{2}\\
&= \frac {a + b}{2}
\end{align*}$
分散とその導出
連続一様分布の分散は、以下のように表されます:
$\begin{align*}V[X] = \frac{(b-a)^2}{12}\end{align*}$
実際に導出してみましょう。
まずは、$E[X^2]$ を求めます。
$\begin{align*}
E[X^2] &= \int_{a}^{b}x^2f(x)dx\\
&= \int_{a}^{b}x^2\frac{1}{b-a}dx\\
&= \frac{1}{b-a}\int_{a}^{b}x^2dx\\
&= \frac{1}{b-a}\left[\frac{x^3}{3}\right]_{a}^{b}\\
&= \frac{1}{b-a}\left(\frac{b^3-a^3}{3}\right)\\
&= \frac{1}{b-a}\frac{(b-a)(b^2+ab+a^2)}{3}\\
&= \frac{b^2+ab+a^2}{3}
\end{align*}$
よって、
$\begin{align*}
V[X] &= E[X^2]-E[X]^2\\
&= \frac{b^2+ab+a^2}{3}-\left(\frac{a+b}{2}\right)^2\\
&= \frac{(b-a)^2}{12}
\end{align*}$
モーメント母関数とその導出
連続一様分布のモーメント母関数は、以下のように表されます:
$\begin{align*}M(t) = E[e^{tX}] = \frac {e^{bt}-e^{at}}{(b-a)t}, \quad -\infty < t < \infty \end{align*}$
実際に導出してみましょう。
$\begin{align*}
M(t) &= \int_{a}^{b}e^{tx}\frac{1}{b-a}dx\\
&= \frac{1}{b-a}\int_{a}^{b}e^{tx}dx\\
&= \frac{1}{b-a}\left[\frac{e^{tx}}{t}\right]_{a}^{b}\\
&= \frac{1}{b-a}\left(\frac{e^{tb}-e^{ta}}{t}\right)\\
&= \frac {e^{bt}-e^{at}}{(b-a)t}
\end{align*}$
まとめ
連続一様分布は、範囲内のどの値も等しい確率で出現する場合に用いられる基本的な確率分布です。期待値や分散が簡単に計算できるため、乱数生成や製造過程など、多くの応用が存在します。

