ベルヌーイ分布とは
ベルヌーイ分布は、成功か失敗、表か裏といったような2つの結果しかない試行(このような試行をベルヌーイ試行といいます)を1回行ったときの特定事象の回数が従う確率分布です。特に、成功確率が $p$ である場合、成功確率 $p$ のベルヌーイ分布といい、$Bin(1, p)$ あるいは $Ber(p)$ と表します。
ベルヌーイ分布に従う確率変数は一般的に「成功(表)のとき1、失敗(裏)のとき0をとる」として定義されます。
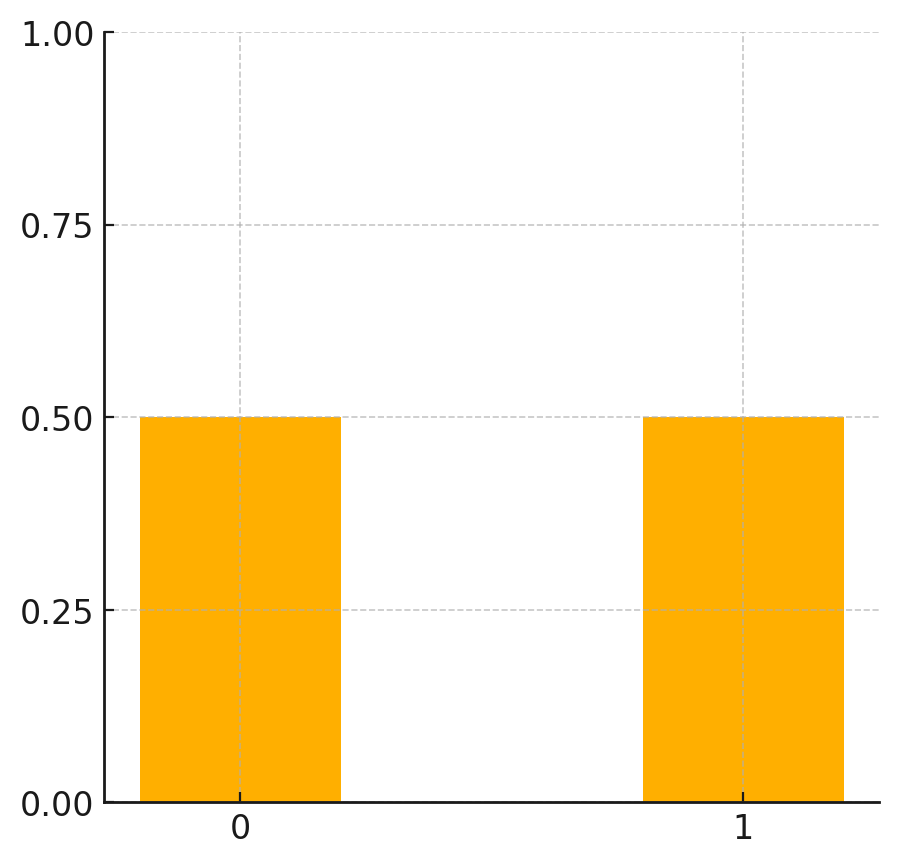
ベルヌーイ分布の例
- コイン投げ
ベルヌーイ分布の典型的な例として、コイン投げが挙げられます。公正なコインの場合、表が出る確率は $p = 0.5$ 、裏が出る確率は $1-p = 0.5$ です。 - 製品の品質チェック
品質管理にベルヌーイ分布を使用することができます。例えば、製品が不良品(失敗)か良品(成功)かを判定するテストがあります。テストに合格する確率はベルヌーイ分布でモデル化され、生産プロセスの改善に役立ちます。
確率関数
ベルヌーイ分布の確率関数は、以下のように表されます:
$P(X=x) = p^x(1-p)^{1-x}, \quad x = 0, 1$
ここで、$P(X = x)$ は確率変数 $X$ が特定の値 $x$ をとる確率を表します。
期待値とその導出
ベルヌーイ分布の期待値は、以下のように表されます:
$E[X] = p$
実際に導出してみましょう。
$\begin{align*}
E[X] &= 1 × p + 0 × (1-p) \\
&= p
\end{align*}$
分散とその導出
ベルヌーイ分布の分散は、以下のように表されます:
$V[X] = p(1-p)$
実際に導出してみましょう。
まずは、$E[X^2]$を求めます。
$\begin{align*}
E[X^2] &= 1 × p + 0 × (1-p) \\
&= p
\end{align*}$
よって、
$\begin{align*}
V[X] &= E[X^2]-E[X]^2 \\
&= p-p^2 \\
&= p(1-p)
\end{align*}$
確率母関数とその導出
ベルヌーイ分布の確率母関数は、以下のように表されます:
$G(s) = E[s^X] = ps + (1-p)$
実際に導出してみましょう。
$\begin{align*}
G(s) &= s × p + s^0 × (1-p) \\
&= ps + (1-p)
\end{align*}$
まとめ
ベルヌーイ分布は、2つの結果しかないシンプルな確率分布ですが、統計学やデータ分析において非常に強力なツールです。コイン投げ、購買行動の予測、品質管理など、多くの実際の問題に適用されるため、その理解は重要です。特に、二項分布や他の複雑な確率分布を学ぶ際の基礎として欠かせないものです。

